Navigation auf uzh.ch
Navigation auf uzh.ch
Die Studie erbrachte vielfältige Ergebnisse über die spezifischen Merkmale der im Unterricht behandelten Aufgaben und ihrer Präsentation. Hier wird eine Auswahl von Ergebnissen zu folgenden Fragen dargestellt.
Nicht aufgeführt werden Ergebnisse der zusätzlichen Analysen zu spezifischen Aspekten der Problemstellung, an welchen sich die Schweiz nicht beteiligt hat (vgl. dazu den internationalen Report und die ausführlichere Publikation).
Mathematische Probleme können entweder unter ausschliesslicher Verwendung der mathematischen Symbolsprache präsentiert werden oder mit einem Bezug zur Alltagswelt der Lernenden.
Abbildung 1 stellt den durchschnittlichen Anteil der Problemstellungen mit und ohne Alltagsbezug pro Lektion dar.
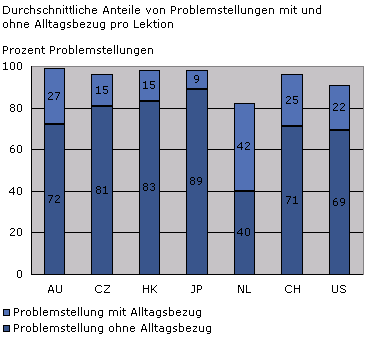
Wie Abbildung 1 deutlich macht, bilden die Problemstellungen, die unter ausschliesslicher Verwendung der spezifisch mathematischen Symbolsprache gegeben werden, in fast allen Ländern klar die Mehrheit der Aufgaben. Eine Ausnahme stellen die niederländischen Lektionen dar. In den niederländischen Lektionen finden sich deutlich weniger Aufgaben, die keinen Alltagsbezug aufweisen. Am wenigsten Aufgaben mit Alltagsbezug finden sich mit 9% in japanischen Lektionen. In australischen, schweizerischen und niederländischen Lektionen ist dieser Anteil deutlich grösser.
Anwendungsaufgaben erfordern die Anwendung von erlernten Prozeduren oder Konzepten auf eine neuartige mathematische Situation. Sie stellen somit höhere Anforderungen als Aufgaben, bei denen lediglich die gleichen Lösungsschritte im gleichen Kontext durchgeführt werden müssen.
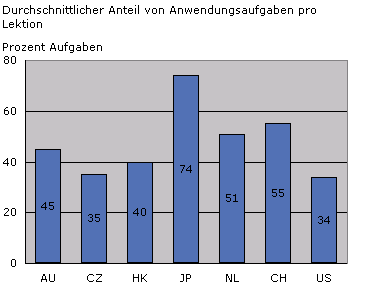
Umgerechnet auf eine Lektion enthalten japanische Lektionen insgesamt deutlich mehr Anwendungsaufgaben als alle anderen Länder, mit Ausnahme der Schweiz.
Dass das Generieren, Vergleichen und Diskutieren von unterschiedlichen Lösungswegen zur Qualität eines verstehensorientierten Unterrichts beiträgt, wird in der aktuellen didaktischen Literatur vielfach betont.
Als Indikator für die Anregung unterschiedlicher Lösungswege wurde bei allen Aufgaben erfasst, ob mehr als ein Lösungsverfahren vor der Klasse präsentiert wurde. Als zweiter Indikator für die Ermutigung zu vielfältigen Lösungswegen wurde für jede Aufgabe erhoben, ob in der Problemstellung explizit darauf hingewiesen wurde, dass die Lernenden selber eine geeignete Lösungsmethode auswählen sollen.

Wie Tabelle 1 zeigt, ist der Anteil von Problemen, zu denen alternative Lösungsmethoden präsentiert werden, in Japan grösser als in anderen Ländern. In Bezug auf die Zahl der Lektionen, in denen mindestens einmal eine Aufgabe mit mehr als einer präsentierten Lösungsmethode vorkommt, bestehen keine Unterschiede. Einzig in den USA weisen signifikant mehr Lektionen mindestens eine solche Aufgabe auf als in Tschechien.
Auch der Anteil an Aufgaben, bei denen alternative Lösungswege nicht notwendigerweise vor der Klasse präsentiert werden, aber in der Aufgabenstellung explizit auf die Wahlmöglichkeit hingewiesen wird, ist, wie Tabelle 2 zeigt, durchwegs recht klein.

Noch seltener als die explizite Wahlmöglichkeit der Lösungsmethode und die Präsentation von verschiedenen Lösungswegen durch die Lehrperson sind Aufgaben, zu denen von den Lernenden selbständig unterschiedliche Lösungswege generiert, vor der Klasse präsentiert und anschliessend diskutiert werden. In Japan erfüllen 9%, in allen anderen Ländern höchstens 3% der Aufgaben dieses Kriterium.